
Comment pouvons-nous fabriquer des panneaux solaires plus performants de 50%? Un adolescent de 13 ans, Aidan Dwyer, a découvert comment les arbres utilisaient les mathématiques (sisi) afin de maximiser la photosynthèse, et l'a appliqué au principe des panneaux solaires.
Pendant une randonnée, il remarque que la disposition des branches des arbres suit une certaine logique, il en déduit (comme le naturaliste Charles Bonnet l'a fait en 1754) que cette tendance suivait
la suite de Fibonacci (hm. "
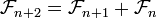
.", mais qui ne la connait pas de tête ? ;) ). Aidan s'est demandé pourquoi ("Oh but why??"), et a pensé qu'il devait y avoir un lien avec la photosynthèse.
Dans une expérience innovante, le jeune chercheur a conçu un faux-chêne doté de panneaux solaires, et a comparé son ensoleillement à celui de capteurs solaires qui peuplent certains toits (cf photo).
Et en fait, son arbre a recueilli 50% d'ensoleillement de plus que l'installation "classique" des panneaux. Concrètement, le soleil tourne, mais les branches sont positionnées de manière à ce qu'il y ait toujours des capteurs ensoleillés.
A quand des arbres photovoltaiques sur votre toit ?
Source :
13-Year-Old Designs Super-Efficient Solar Array Based on the Fibonacci Sequence
 Comment pouvons-nous fabriquer des panneaux solaires plus performants de 50%? Un adolescent de 13 ans, Aidan Dwyer, a découvert comment les arbres utilisaient les mathématiques (sisi) afin de maximiser la photosynthèse, et l'a appliqué au principe des panneaux solaires.
Pendant une randonnée, il remarque que la disposition des branches des arbres suit une certaine logique, il en déduit (comme le naturaliste Charles Bonnet l'a fait en 1754) que cette tendance suivait la suite de Fibonacci (hm. "
Comment pouvons-nous fabriquer des panneaux solaires plus performants de 50%? Un adolescent de 13 ans, Aidan Dwyer, a découvert comment les arbres utilisaient les mathématiques (sisi) afin de maximiser la photosynthèse, et l'a appliqué au principe des panneaux solaires.
Pendant une randonnée, il remarque que la disposition des branches des arbres suit une certaine logique, il en déduit (comme le naturaliste Charles Bonnet l'a fait en 1754) que cette tendance suivait la suite de Fibonacci (hm. "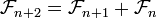 .", mais qui ne la connait pas de tête ? ;) ). Aidan s'est demandé pourquoi ("Oh but why??"), et a pensé qu'il devait y avoir un lien avec la photosynthèse.
Dans une expérience innovante, le jeune chercheur a conçu un faux-chêne doté de panneaux solaires, et a comparé son ensoleillement à celui de capteurs solaires qui peuplent certains toits (cf photo).
Et en fait, son arbre a recueilli 50% d'ensoleillement de plus que l'installation "classique" des panneaux. Concrètement, le soleil tourne, mais les branches sont positionnées de manière à ce qu'il y ait toujours des capteurs ensoleillés.
A quand des arbres photovoltaiques sur votre toit ?
Source : 13-Year-Old Designs Super-Efficient Solar Array Based on the Fibonacci Sequence
.", mais qui ne la connait pas de tête ? ;) ). Aidan s'est demandé pourquoi ("Oh but why??"), et a pensé qu'il devait y avoir un lien avec la photosynthèse.
Dans une expérience innovante, le jeune chercheur a conçu un faux-chêne doté de panneaux solaires, et a comparé son ensoleillement à celui de capteurs solaires qui peuplent certains toits (cf photo).
Et en fait, son arbre a recueilli 50% d'ensoleillement de plus que l'installation "classique" des panneaux. Concrètement, le soleil tourne, mais les branches sont positionnées de manière à ce qu'il y ait toujours des capteurs ensoleillés.
A quand des arbres photovoltaiques sur votre toit ?
Source : 13-Year-Old Designs Super-Efficient Solar Array Based on the Fibonacci Sequence












